(대학수학) 극좌표계 문제는 어떻게 해결하는지 알아보자.

1. 극좌표계

극좌표계는 좌표계를 발명한 데카르트로부터 시작하여 17c 중반 그레구아르 생뱅상, 보나벤투라 카발리에리에 의해 독자적으로 극좌표계를 설명하였다. 카발리에리는 아르키메데스 나선의 넓이를 구하기 위해 사용하였다. 이후 뉴턴 등 수많은 수학자들이 극좌표계에 관한 연구결과를 발표한다.

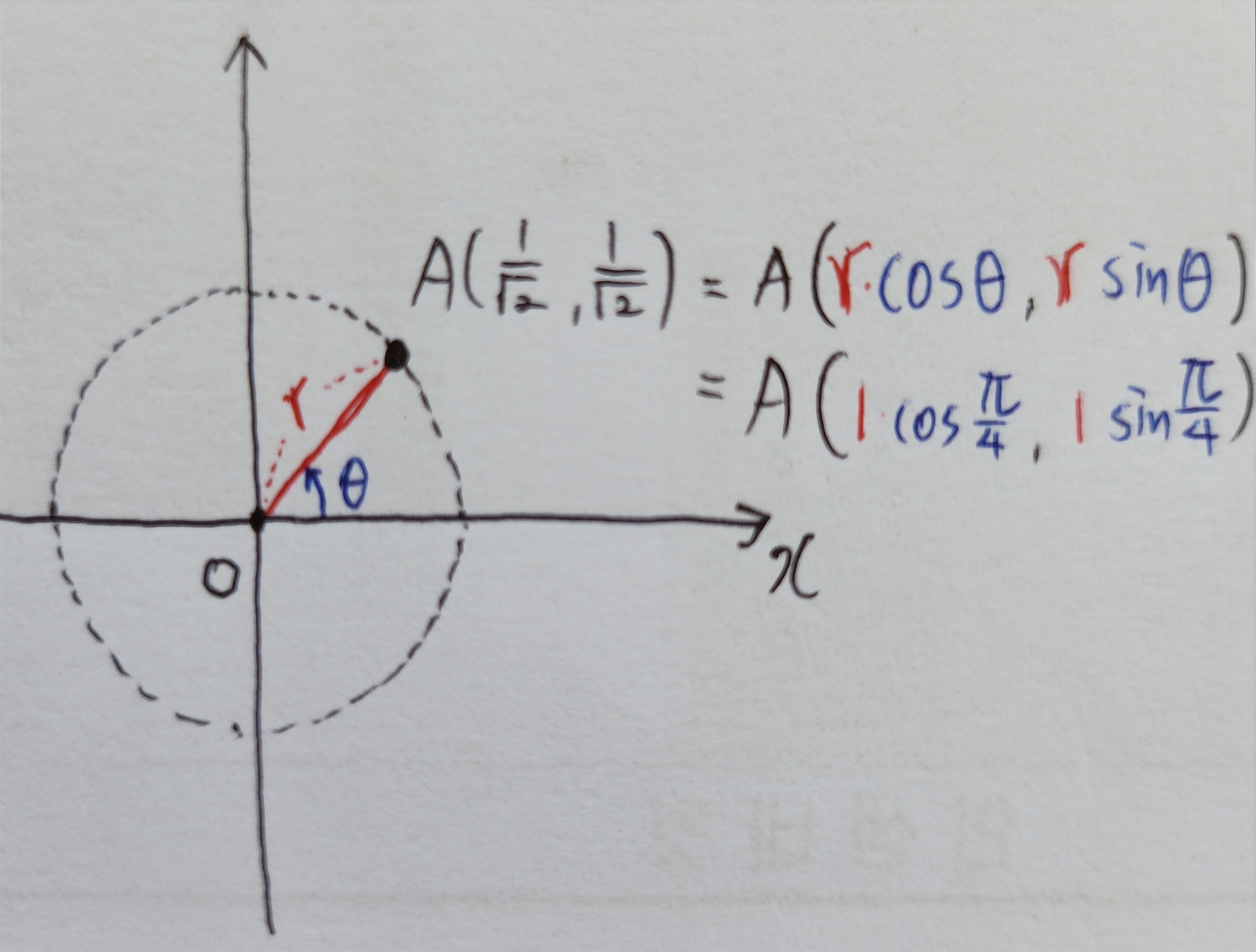
극좌표계는 좌표평면 위의 점(x, y)을 원점과 이은 길이 r,  x축의 양의 방향으로부터 점까지의 동경 (세타)로 표현하는 방법이다. (아래 예시와 같이)

2. 극좌표계 대표문제

극좌표계 대표문제를 해석해 보자.

(1) 극좌표계 관계식을 해석하기
   세타값에 따라 r값이 달라지는 관계식이다. 세타=0이면 r=0, 세타=90도이면 r=1, 세타=180도이면 r=2  등등 세타값에 따라 점을 찍어주면 다음과 같은 곡선이 만들어진다.

   그래프를 잘 못 그리므로 지오지브라를 이용해 보자.

90도 회전한 하트모양이 나온다.

(2) 곡선의 길이, 둘러싸인 넓이 구하기

(3) 곡선으로 둘러싸인 영역의 넓이
곡선의 길이를 구하니 힘이 들어 넓이는 다음에 구해야겠다. 영역의 넓이는 x와 y에 관한 이중적분으로 해결해야 하며 r과 세타로 변수변환을 하면서 자코비값을 곱해주고 적분계산을 하면 된다. 풀어보아라.

3. 첨언

극좌표계는 고등과정에서도 등장한다. 뿐만 아니라 곡선, 곡면에 관한 해석에서 극좌표계로 변환하여 해석하는 경우가 많으므로 꼭 공부해야 할 수학 영역이라 할 수 있다.